Introduction
I believe there are already many introductions to linear logic. Linear types, while not a fad, are familiar to some programmers.
The geometry of interaction was Girard’s next major project after introducing linear logic. He even wrote a series of 6 papers about it (known as GoI 1 to 6 — although there is also a GoI 0 for connoisseurs and a more philosophical paper with forgotten ideas called Towards a geometry of interaction).
I did two master’s theses on the subject and I had a hard time understanding anything at first. Girard’s papers were difficult to read. I had almost no background in mathematics. It didn’t help that those who did understand the main ideas reformulated them in different terms, creating independent subcultures of GoI, the most common ones are:
- traced symmetric monoidal categories (Abramsky, Haghverti, Scott);
- abstract machines for executing lambda-terms (Danos, Regnier, Laurent, Asperti).
Since I’m French, I understood the GoI as a method for normalizing lambda-terms in a space-efficient way by only following paths in an alternative graph-like representation. Although valid, the most common interpretations lose sight of Girard’s original motivation.
Origin
The original GoI was an abstraction of proofs aiming at explaining logic without any primitive reference to logic. What remains when you strip formal proofs completely naked, without all the semantic scaffolding? What is logic when you don’t assume that logical rules descend from the sky?
A formal proof is usually described as a sequence of logical rules applied until you reach your conclusion.

But formal proofs are not “static” objects — They live. When you explain something to someone, that explanation is itself a kind of proof of some assertion. But it uses shortcuts (called cuts in proof theory) that can be expanded upon if someone asks you to explain more precisely — a process known as cut-elimination procedure. In programming, this corresponds to having function calls then inlining the function bodies to get a direct connection.
Proof-nets
In practice, statements are further decomposed into atomic statements linked with connectives that build new meanings from components.
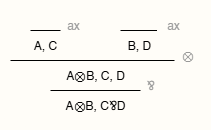
Now, forget that we are representing proofs that manipualte formulas or assertions. Forget that these symbols may have a meaning. Rules are just ways of rearranging symbols in space. Another way to represent proofs — one that ignores the order in which rules are applied — is called proof-nets. They simply show how rules act on formulas in a graph-like manner. At this stage, formulas don’t matter at all — we could replace them with any identifiers.
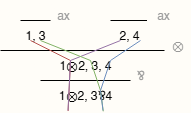

Getting rid of semantics
However, this is still not the best representation of proofs. We have artificially removed references to logic. Proof-nets are correct because they come directly from translations of proofs which are themselves correct by the “great magical laws of logic”. It’s like the circularity of a dictionary: defining words in terms of other words without ever directly grasping the underlying concept.
Girard tried to do some reverse-engineering: given an arbitrary graph that looks like a proof-net, how do you know it is correct, i.e. whether it comes from our ealier notion of proof (how do you go from meaningless to meaningful?).
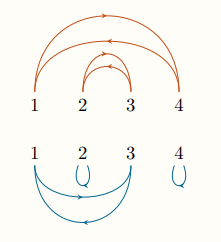
To answer that question, he introduced what he called a correctness criterion. We can imagine a current flowing inside a proof-net (as if it was an electrical circuit). Connectives can yield several combinations of flow direction.
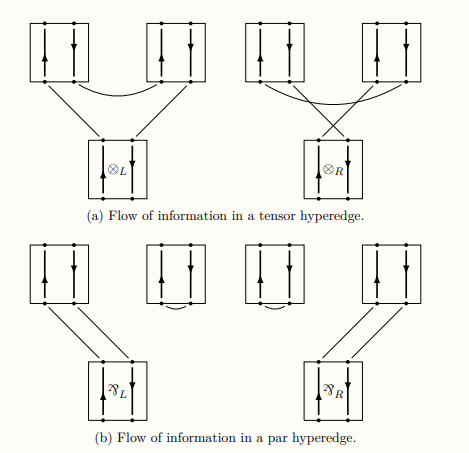
It turns out that our graphs are correct when their underlying flows form one big closed circuit passing through all nodes (what Girard calls a long trip, in contrast to short trips which are like short-circuits).
Even researchers in linear logic don’t always notice this, but it’s something very special: we made the shape of logical correctness explicit. We’ve stepped outside purely linguistic definitions
Homogeneous decomposition
The GoI shows that proof-nets are actually composite objects: a core part (that Girard calls “vehicle”) can be extracted. It describes a flow between atomic formulas.
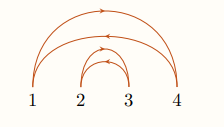
The idea is then to not see proofs as static objects but to reason in terms of actions on that core part:
- cut-elimination rewires those flows (this corresponds to execution in programming);
- a correctness criterion checks the validity of proofs (this corresponds to type checking in programming).
Each of these actions can also be described purely in terms of flow between atomic formulas as well. They actually represent a sufficient for describing proofs. These flow descriptions can be formalized as permutations or graphs (in Seiller’s interpretation) over sets of natural numbers.
Let’s call these flow descriptions interaction graphs (following Seiller’s terminology). When performing cut-elimination, you actually place your vehicle against another interaction graph representing cuts. Then you can compute their interaction (or execution) by computing maximal alternating paths.
What’s beautiful is that correctness criteria follow the same principle. Checking validity is actually a special case of cut-elimination — you place the vehicle against a suitable set of interaction graphs that serve as tests. If cut elimination is about making things interact, validity checking is about testing against a representative set of cases that ensure sound behavior for all objects of that “shape”.
In programming terms, they are tests.
We make the vehicle interact with all tests and expect a certain result (just as Girard’s long trips describe).
Extension
This gives us a sufficient and very elementary representation of proofs. We operate in a world of simple interactive objects, like LEGO bricks. Some represent the computational core of a proof, some represent execution configurations, and others represent specification tests.
However, this description applies only to the most basic fragment of linear logic: multiplicative linear logic (MLL). Girard did not introduce GoI incrementally — he went straight to the full generalization in his first GoI paper.
The complication arises when formulas can be duplicated. There may be several related occurrences of the same formula. Mathematically, this means having to deal with infinite permutations (or matrices, since permutations can be represented as matrices). This is why Girard needed Hilbert spaces, and later more complex operator algebras.
In GoI 3, Girard observed that his work with operator algebras could be simulated using first-order terms and the resolution rule (based on term unification, as in logic programming). This opened the path for later developments by Bagnol, Aubert, and Pistone, and eventually Girard’s final “transcendental syntax” project, first introduced in GoI 6.
Thomas Seiller, a specialist in GoI, describes Girard’s entire program in terms of graphs — interaction graphs and later graphings, which connect to mathematical fields such as dynamical systems, algebraic geometry, and ergodic theory.
Geometry of interaction as a model
There are several experiments in the GoI projects starting from different points:
- permutations and matrices;
- operator algebras;
- partitions on a set of natural numbers;
- interaction graphs;
- terms and unification.
We can then see GoI as a model or framework describing both computation and validity (type) checking in a uniform way without reference to semantics.
Legacy
Although Girard’s original motivation has often been forgotten, the technical developments of GoI have led to several widely studied results. These are now so common that they are often what people mean when they say geometry of interaction.
Token machine and space-efficient computation
By the proofs-as-programs correspondence, simply typed lambda-calculus (STLC) corresponds to natural deduction for minimal logic and this correspondence extends to functional programming.
Similarly, proof-nets can encode typed lambda-terms. One application of GoI is that cut elimination (term normalization) can be performed by following paths in a proof-net, giving a space-efficient way to execute a graph-like representation of programs.
GoI can also be adapted to work directly on term graphs instead of their proof-net representations.
Interaction nets and combinators
Lafont introduced a generalization of proof-nets called interaction nets, essentially a way of representing rewriting rules through graph rewriting.
What is especially remarkable is that all rules can be defined using just three combinators (called interaction combinators) and six associated rules.
Interaction nets can express the optimal reduction of lambda calculus, as presented by Lamping and independently by Lévy.
They have also been used by “Victor Taelin” in the HVM project, leveraging their massively parallel nature (among other things) to develop the languages Kind and Bend.
Conclusion
The geometry of interaction is not merely a method or a clever trick, but a deep analysis and reverse-engineering of formal proofs and of what it means to be logically correct.
It opens up logic, allowing us to study it beyond its usual frontiers, and transforms it into more than just a cold science of symbols. It makes it about shapes of subjective validity, and about the mechanisms of certainty and anticipation.
The final article on GoI introduces its direct successor, the transcendental syntax, which extends the GoI 3 approach of interpreting linear logic with terms and unification, providing a purely finite and effective definition of logic. This framework explores, both technically and philosophically, the nature of logical rules and systems at their deepest level.
Acknowledgement
I would like to thank my dear friend ChatGPT for helping make my English more understandable.